Aerodynamics Module

This module contains a library of classes devoted to modeling aircraft parts.

The main purpose of this library is to model various types of aircraft parts. Currently only wing objects are suported, however in the future it is possible that fuselages as well as other parts will be added.

SUMARRY OF THE METHODS:  

• K: The kernel function used in the doublet-lattice method to relate

  downwashes to panel pressures.

• calcAIC: Provided several vectors of numbers as well as a reduced frequency

  and mach number, this method calculates a matrix of AIC’s using doublet- lattice method elementary solutions. This method is used by the FEM class flutterAnalysis method.

SUMARRY OF THE CLASSES:  

• Airfoil: Primarily used for the generation of structural cross-sectional

  meshes, this class represent an airfoil. This class could be expanded in future to use simple 2D panel methods for an airfoil of arbitrary shape.

• CQUADA: This class creates quadrilateral panels intended to be used for

  potential flow panel methods. Currently it is used for the unsteady doublet-lattice panels.

• CAERO1: This class is used to generate a lattice of CQUADA panels.

DOUBLET-LATTICE KERNEL FUNCTION

AeroComBAT.Aerodynamics.K()

Evaluates the doublet-lattice kernel function.

Provided several geometric parameters about the sending and recieving panels, this method evaluates the kernel function which relates the pressure on one panel to the downwash induced at another panel.

Args:

• Xr (1x3 np.array[float]): The location of the recieving point.

• Xs (1x3 np.array[float]): The location of the sending point.

• gamma_r (1x3 np.array[float]): The dihedral of the panel corresponding

  to the recieving point.

• gamma_s (1x3 np.array[float]): The dihedral of the panel corresponding

  to the sending point.

• M (float): The mach number

• br (float): The reference semi-chord

• kr (float): The reduced frequency

• r1 (float): The scalar distance between the sending point and the

  recieving point.

Returns:

• Kbar (complex128): The evaluation of the unsteady kernel function which

  is complex in nature.

DOUBLET-LATTICE AIC METHOD

AeroComBAT.Aerodynamics.calcAIC()

Calculate the doublet-lattice AIC’s.

Provided the geometry of all of the doublet-lattice panels, this method calculates the AIC matrix.

Args:

• M (float): The mach number.

• kr (float): The reduced frequency.

• br (float): The reference semi-chord.

• delta_x_vec (1xN array[float]: An array of chord length of the panels.

• sweep_vec (1xN array[float]): An array of sweep angles of the panels.

• l_vec (1xN array[float]): An array of average doublet line lengths of

  the panels.

• dihedral_vec (1xN array[float]): An array of dihedral angles of the

  panels.

• Xr_vec (Nx3 np.array[float]): A matrix of recieving points, where a row

  are the 3D coordinates of the point.

• Xi_vec (Nx3 np.array[float]): A matrix of inboard sending points, where

  a row are the 3D coordinates of the point.

• Xc_vec (Nx3 np.array[float]): A matrix of center sending points, where

  a row are the 3D coordinates of the point.

• Xo_vec (Nx3 np.array[float]): A matrix of outboard sending points,

  where a row are the 3D coordinates of the point.

• symxz (bool): A boolean operater intended to determine whether or not

  a reflection of the panels should be considered over the xz-plane.

Returns:

• D (NPANxNPAN np.array[complex128]): The matrix which relates pressures

  over panels to induced velocities over those panels. In more simple terms, this is the inverse of the desired AIC matrix.

AIRFOIL

class AeroComBAT.Aerodynamics.Airfoil(c, **kwargs)

Creates an airfoil object.

This class creates an airfoil object. Currently this class is primarily used in the generation of cross-sectional meshes. Currently only NACA 4 series arfoil and rectangular boxes are supported.

Attributes:

• c (float): The chord length of the airfoil.

• t (float): The max percent thickness of the airfoil.

• p (float): The location of the max camber of the airfoil, in 10%

  increments.

• m (float): The max camber of the airfoil as a percent of the chord.

Methods:

• points: Generates the x and y upper and lower coordinates of the

  airfoil.

__init__(c, **kwargs)

Airfoil object constructor.

Initializes the airfoil object.

Args:

• c (float): The chord length of the airfoil.

• name (str): The name of the airfoil section. This can either be

  a ‘NACAXXXX’ airfoil or ‘box’ which signifies the OML is a rectangle.

Returns:

• None

points(x)

Generates upper and lower airfoil curves.

This method will generate the x and y coordinates for the upper and lower airfoil surfaces provided the non-dimensional array of points x.

Args:

• x (1xN np.array[float]): An array of floats for which the upper and

  lower airfoil curves should be generated.

Returns:

• xu (1xN np.array[float]): The upper x-coordinates of the curve.
• yu (1xN np.array[float]): The upper y-coordinates of the curve.
• xl (1xN np.array[float]): The lower x-coordinates of the curve.
• yl (1xN np.array[float]): The lower y-coordinates of the curve.

printSummary(x)

A method for printing a summary of the airfoil object.

Prints the airfoil chord length as well as airfoil name.

Args:

• None

Returns:

• (str): Prints the tabulated chord length and name of the airfoil

CQUADA

class AeroComBAT.Aerodynamics.CQUADA(PANID, xs)

Represents a CQUADA aerodynamic panel.

This CQUADA panel object is used for the unsteady aerodynamic doublet- lattice method currently, although it could likely easily be extended to support the vortex lattice method as well. The geometry of a generic panel can be seen in the figure below.

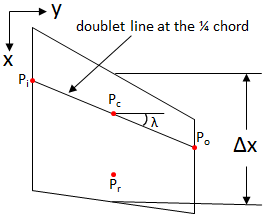
Attributes:

• type (str): The type of object.

• PANID (int): The integer ID linked with the panel.

• xs (1x4 np.array[float]): The x coordinates of the panel.

• ys (1x4 np.array[float]): The y coordinates of the panel.

• zs (1x4 np.array[float]): The z coordinates of the panel.

• DOF (dict[NID,factor]): This dictionary is for connecting the movement

  of the panel to the movement of an associated structure. Since a panel’s control point could be between two nodes (in the middle of an element), the position of the panel can interpolated using a finite element formulation. The NID’s link the movement of the panel to the movement of a corresponding node. The factor allows for a finite element interpolation.

• Area (float): The area of the panel.

• sweep (float): The average sweep of the panel’s doublet line.

• delta_x (float): The average chord line of the panel.

• l (float): The length of the panel’s doublet line.

• dihedral (float): The dihedral of the panel.

• Xr (1x3 np.array[float]): The coordiantes of the panel’s sending point.

• Xi (1x3 np.array[float]): The coordinates of the panel’s inboard

  sending point.

• Xc (1x3 np.array[float]): The coordinates of the panel’s center

  sending point.

• Xo (1x3 np.array[float]): The coordinates of the panel’s outboard

  sending point.

Methods:

• x: Provided the non-dimensional coordinates eta and xi which go from -1

  to 1, this method returns corresponding the x coordinates.

• y: Provided the non-dimensional coordinates eta and xi which go from -1

  to 1, this method returns corresponding the y coordinates.

• z: Provided the non-dimensional coordinates eta and xi which go from -1

  to 1, this method returns corresponding the z coordinates.

• J:Provided the non-dimensional coordinates eta and xi which go from -1

  to 1, this method returns the jacobian matrix at that point. This method is primarily used to fascilitate the calculation of the panels area.

• printSummary: Prints a summary of the panel.

Note

The ordering of the xs, ys, and zs arrays should be ordered in a

finite element convention. The first point refers to the root trailing edge point, followed by the tip trailling edge, then the tip leading edge, then root leading edge.

J(eta, xi)

Calculates the jacobian at a point in the element.

This method calculates the jacobian at a local point within the panel provided the master coordinates eta and xi.

Args:

• eta (float): The eta coordinate in the master coordinate domain.*
• xi (float): The xi coordinate in the master coordinate domain.*

Returns:

• Jmat (3x3 np.array[float]): The stress-resutlant transformation

  array.

Note

Xi and eta can both vary between -1 and 1 respectively.

__init__(PANID, xs)

Initializes the panel.

This method initializes the panel, including generating many of the geometric properties required for the doublet lattice method such as Xr, Xi, etc.

Args:

• PANID (int): The integer ID associated with the panel.

• xs (1x4 array[1x3 np.array[float]]): The coordinates of the four

  corner points of the elements.

Returns:

• None

printSummary()

A method for printing a summary of the CQUADA panel.

Prints out a tabulated information about the panel such as it’s panel ID, and the coordinates of it’s four corner points.

Args:

• None

Returns:

• summary (str): The summary of the CQUADA attributes.

x(eta, xi)

Calculate the x-coordinate within the panel.

Calculates the x-coordinate on the panel provided the desired master coordinates eta and xi.

Args:

• eta (float): The eta coordinate in the master coordinate domain.*
• xi (float): The xi coordinate in the master coordinate domain.*

Returns:

• x (float): The x-coordinate within the element.

Note

Xi and eta can both vary between -1 and 1 respectively.

y(eta, xi)

Calculate the y-coordinate within the panel.

Calculates the y-coordinate on the panel provided the desired master coordinates eta and xi.

Args:

• eta (float): The eta coordinate in the master coordinate domain.*
• xi (float): The xi coordinate in the master coordinate domain.*

Returns:

• y (float): The y-coordinate within the element.

Note

Xi and eta can both vary between -1 and 1 respectively.

z(eta, xi)

Calculate the z-coordinate within the panel.

Calculates the z-coordinate on the panel provided the desired master coordinates eta and xi.

Args:

• eta (float): The eta coordinate in the master coordinate domain.*
• xi (float): The xi coordinate in the master coordinate domain.*

Returns:

• z (float): The z-coordinate within the element.

Note

Xi and eta can both vary between -1 and 1 respectively.

CAERO1

class AeroComBAT.Aerodynamics.CAERO1(SID, x1, x2, x3, x4, nspan, nchord, **kwargs)

Represents an aerodynamic surface.

This CAERO1 object represents an aerodynamic lifting surface to be modeled using the doublet-lattice method.

Attributes:

• type (str): The type of object.

• SID (int): The integer ID linked with the surface.

• xs (1x4 np.array[float]): The x coordinates of the panel.

• ys (1x4 np.array[float]): The y coordinates of the panel.

• zs (1x4 np.array[float]): The z coordinates of the panel.

• mesh ((NPAN+1)x(NPAN+1) np.array[int]): The panel ID’s in the relative

  positions of their corresponding panels.

• xmesh ((NPAN+1)x(NPAN+1) np.array[float]): The x-coordinates of the

  lifting surface nodes.

• ymesh ((NPAN+1)x(NPAN+1) np.array[float]): The y-coordinates of the

  lifting surface nodes.

• zmesh ((NPAN+1)x(NPAN+1) np.array[float]): The z-coordinates of the

  lifting surface nodes.

• CQUADAs (dict[PANID, CQUADA]): A dictionary mapping panel ID’s to

  CQUADA panel objects.

Methods:

• x: Provided the non-dimensional coordinates eta and xi which go from -1

  to 1, this method returns corresponding the x coordinates.

• y: Provided the non-dimensional coordinates eta and xi which go from -1

  to 1, this method returns corresponding the y coordinates.

• z: Provided the non-dimensional coordinates eta and xi which go from -1

  to 1, this method returns corresponding the z coordinates.

• plotLiftingSurface: Plots the lifting surface in 3D space. Useful for

  debugging purposes.

• printSummary: Prints a summary of the panel.

Note

The ordering of the xs, ys, and zs arrays should be ordered in a

finite element convention. The first point refers to the root leading edge point, followed by the root trailling edge, then the tip trailing edge, then tip leading edge.

__init__(SID, x1, x2, x3, x4, nspan, nchord, **kwargs)

Constructor for the CAERO1 lifting surface object.

Provided several geometric parameters, this method initializes and discretizes a lifting surface using CQUADA panel objects.

Args:

• SID (int): The integer ID for the surface.

• x1 (1x3 np.array[float]): The coordinate of the root leading edge.

• x2 (1x3 np.array[float]): The coordinate of the root trailing edge.

• x3 (1x3 np.array[float]): The coordinate of the tip trailing edge.

• x4 (1x3 np.array[float]): The coordinate of the tip leading edge.

• nspan (int): The number of panels to run in the spanwise direction.

• nchord (int): The number of panels to run in the chordwise

  direction.

Returns:

• None

plotLiftingSurface(**kwargs)

Plots the lifting surface using the MayaVi environment.

This method plots the lifting surface using the MayaVi engine. It is most useful for debugging models, allowing the user to verify that the wing they thought they generated is actually what was generated.

Args:

• figName (str): The name of the figure

Returns:

• (figure): MayaVi Figure of the laminate.

printSummary()

A method for printing a summary of the CAERO1 element.

Prints out the surface ID, as well as the number of chordwise and spanwise panels.

Args:

• None

Returns:

• summary (str): A summary of the CAERO1 surface attributes.

x(eta, xi)

Calculate the x-coordinate within the lifting surface.

Calculates the x-coordinate within the lifting surface provided the desired master coordinates eta and xi.

Args:

• eta (float): The eta coordinate in the master coordinate domain.*
• xi (float): The xi coordinate in the master coordinate domain.*

Returns:

• x (float): The x-coordinate within the element.

Note

Xi and eta can both vary between -1 and 1 respectively.

y(eta, xi)

Calculate the y-coordinate within the lifting surface.

Calculates the y-coordinate within the lifting surface provided the desired master coordinates eta and xi.

Args:

• eta (float): The eta coordinate in the master coordinate domain.*
• xi (float): The xi coordinate in the master coordinate domain.*

Returns:

• y (float): The y-coordinate within the element.

Note

Xi and eta can both vary between -1 and 1 respectively.

z(eta, xi)

Calculate the z-coordinate within the lifting surface.

Calculates the z-coordinate within the lifting surface provided the desired master coordinates eta and xi.

Args:

• eta (float): The eta coordinate in the master coordinate domain.*
• xi (float): The xi coordinate in the master coordinate domain.*

Returns:

• z (float): The y-coordinate within the element.

Note

Xi and eta can both vary between -1 and 1 respectively.